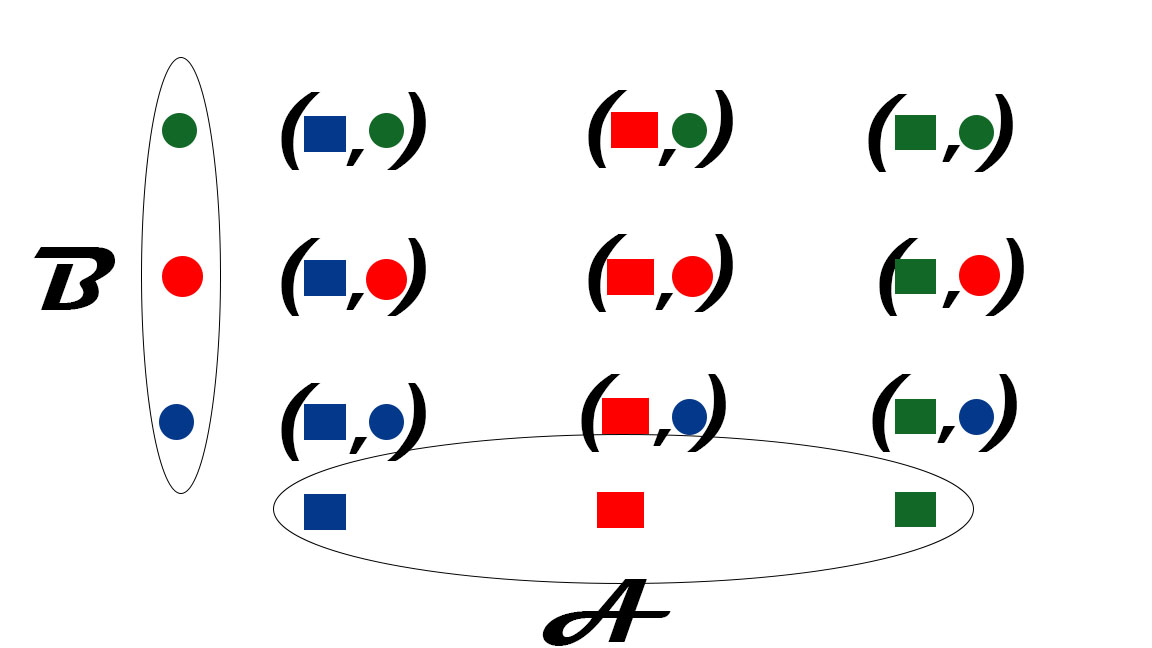
Oheisen kuvan mukaisesti kahdesta kolmearvoisesta joukosta voidaan muodostaa yhdeksän erilaista arvoparia. Tällainen vaihtoehtojen määrä on vielä hallittavissa, mutta entä jos lukujoukkoja on paljon suurempi määrä? Kuvitellaan tilanne, jossa lukujoukkoja on kahden sijasta yhdeksän, niillä jokaisella on kolmen sijaan kuusi erilaista mahdollista arvoa ja pitäisi muodostaa arvoparien sijaan yhdeksän arvon ryhmiä, joihin jokaiseen pitäisi saada mukaan yksi arvo jokaisesta yhdeksästä lukujoukosta? Lisäksi yhdeksän arvon ryhmän tulisi edustaisi mahdollisimman tarkasti 60 prosenttia kokonaismäärästä. Tämä kuviteltu tilanne on ihan todellinen ja parhaan vaihtoehdon valinta pitäisi tehdä miljoonien joukosta.
Mitä ongelmaa ratkaistiin ja miksi?
- Palkeiden kautta kulkee vuosittain yli neljä miljoonaa asiakasvirastojen maksusuoritetta, jotka ohjataan useaan eri pankkiin. Maksuliikelajeja (kuten palkka) on kuutta erilaista ja asiakasvirastoja lähes 70. Asiakasviraston yksittäisen maksuliikelajin on ohjauduttava samaan pankkiin, mutta asiakasviraston kaikki maksuliikkeet eivät voi olla yhden pankin varassa.
- Haluttiin selvittää, kuinka Palkeiden monimutkainen maksuliike kannattaa järjestää. Pankeille tuli antaa arvio heidän kautta kulkevien suoritteiden määrästä (suhteessa kokonaismäärään).
- Kaikkia miljoonia vaihtoehtoja olisi mahdotonta vertailla ja arvioida ilman ohjelmallista optimointia.
Mitä tehtiin?
- Kaikki eri vaihtoehdot voidaan selvittää tilastollista ohjelmistoa hyödyntäen karteesisen tulon lausekkeella. Analytiikan keinoin voidaan rajata tilanteeseen soveltuvien vaihtoehtojen määrä pieneksi joukoksi.
- Palkeiden tapauksessa selvitettiin kaikki mahdolliset yhdistelmävaihtoehdot ja niille suhteelliset osuudet maksusuoritteiden kokonaismäärästä. Yhdistelmävaihtoehdot laitettiin järjestykseen sen mukaan, kuinka lähellä pankkikohtainen suoritteiden määrä oli tavoiteltua suhteellista osuutta.
Tulokset
- Saaduista vaihtoehdoista voidaan ottaa jatkotarkasteluun niitä, jotka parhaiten vastaavat haluttuun tarpeeseen.
- Palkeiden tapauksessa tarkasteluun otettiin viisi osuvinta, joista jokainen johti tavoiteltuun kokonaismääräosuuteen yhden prosentin tuhannesosan tarkkuudella.
- Viittä vaihtoehtoa peilattiin toissijaisiin tavoitteisiin, joiden osalta ne poikkesivat huomattavasti toisistaan. Kun vaihtoehtojen joukko oli seulottu näin pieneksi, jatkovertailu oli asiakkaan itsensäkin helposti toteutettavissa.
Mitä seuraavaksi?
- Tilastollisella ohjelmalla voidaan pienentää helpommin hahmotettavaksi mitä tahansa vaihtoehtojen joukkoa.
Haluatko kuulla lisää tai keskustella mahdollisesta yhteistyöstä?
Haluatko kuulla enemmän analysointipalveluista ja sen mahdollisuuksista? Tutustu tarkemmin Palkeiden analyysipalveluihin.
Ota yhteyttä: analysointipalvelut@palkeet.fi